以弹簧为模型讨论,当考虑空气阻力时,运动方程为 \[ ma = -kx - bv \] 阻尼系数\(b\)可以随时间变化
- 阻尼振动的结果
振动为周期运动,周期由劲度系数\(k\)和阻尼系数\(b\)共同决定 \(\omega = \sqrt{\dfrac{k}{m}}\rightarrow \omega_N = \sqrt{\dfrac{k}{m}-\dfrac{\gamma^2}{4}}\)
振幅随时间减小
\(A \rightarrow A_N = Ae^{-\gamma t / 2}\)
图像表示
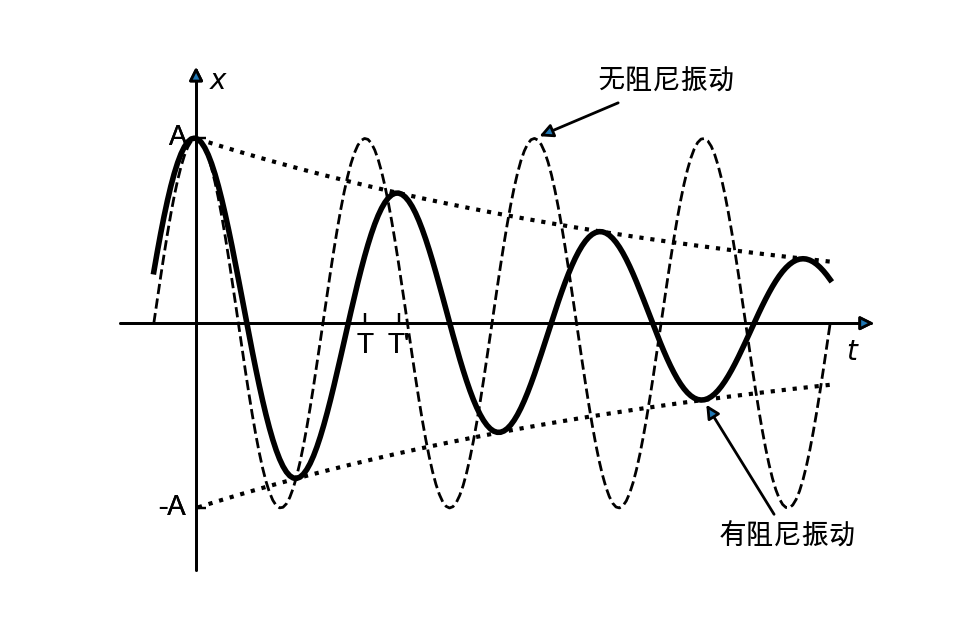
定量分析
运动方程可以改写为
\(\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega^2x = 0\), \(\gamma=\dfrac{b}{m}\)和\(\omega=\sqrt{\dfrac{k}{m}}\)
考虑同形式的复数方程
\(\dfrac{d^2Z}{dt^2} + \gamma\dfrac{dZ}{dt} + \omega^2Z = 0\),
\(Z\) 的实数部分即为阻尼方程的解。
令\(Z = Ce^{At}\),\(A\)和\(C\)为复常数,代入上式得到\(A\)的方程
\(A^2 + \gamma A + \omega^2 = 0\)
\(A\)的解为\(A=-\gamma/2\pm i\sqrt{\omega^2-\dfrac{\gamma^2}{4}}\), 假设阻力不大,即\(\omega\gt\gamma/2\)
- \(Z\)的通解为\(Z=e^{-\gamma t/2}(C_1e^{+i\omega_N t} + C_2e^{-i\omega_N t})\)
故阻尼方程的解为
\(x = Re(Z) = e^{-\gamma t/2}[D\cos(\omega_N t) - E\sin(\omega_N t)]\),\(D\) 和 \(E\) 为常数。
令初始相位为\(\theta_0=\tan^{-1}(\dfrac{D}{E})\),\(L=\sqrt{D^2-E^2}\),\(x\)可以化简为
\(x = Le^{-\gamma t/2}\cos(\omega_N t + \theta_0)\)


